How NOT to build a sequence-to-sequence translator
Sequence-to-sequence language models have achieved a number of high-profile successes lately, from neural language translation to (most recently) OpenAI’s GPT-3. My attention piqued by AI Dungeon and reading a bunch of Jay Alammar’s blog posts, I thought I would try my hand at implementing my own seq2seq model from scratch. And then everything went horribly wrong.
Some background
If you have the time, I strongly endorse reading some of the prominent papers in the subject, or at least Jay’s relevant blog posts. About halfway through this project, I also discovered PyTorch’s seq2seq+attention tutorial, which helped me correct some (but not all!) of my mistakes.
“But Matt, I’d rather read your parroted explanations of RNNs than some peer-reviewed expertly written swill from arXiv!”, you say. Well, dear reader, here it goes.
A single-layer feedforward neural net with activation $\sigma$ looks like this:
\[x^{i} \mapsto \sigma \left( W_{ij} x^{i} + \beta_{j} \right),\]where $W$ denotes the layer’s weights and $\beta$ its bias (I am using Einstein summation notation to describe this operation). Stacking sequences of these transformations together defines an extremely simple type of neural net (a multi-layer perceptron). Let $f:\mathbb{R}^{N + H} \rightarrow \mathbb{R}^{M + H}$ denote such a neural net. Then, for any sequence of vectors $(x_0, x_1, \ldots, x_k)$, we can turn $f$ into a recurrent neural net by introducing a vector $h_{t} \in \mathbb{R}^{H}$ (the “hidden state”), and defining the output of our recurrent network as follows:
\[(y_{t}, h_{t+1}) := f(x_{t}, h_{t})\]and setting some initial “hidden state” (often $h_0 = 0$). (To be ridiculously pedantic, I’m applying the isomorphism between $\mathbb{R}^{N} \times \mathbb{R}^{H}$ and $\mathbb{R}^{N + H}$ otherwise known as concatenation.)
This is sometimes depicted “unrolled”, with each step in the sequence shown explicitly:
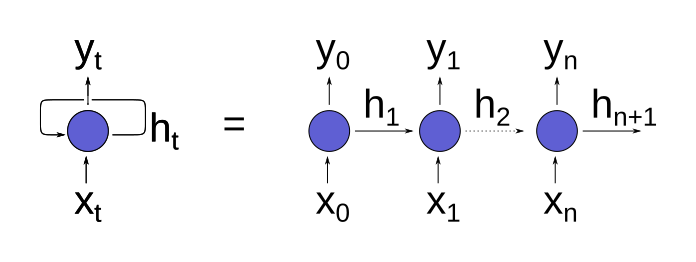
Recurrent neural nets are useful because they are stateful: the vector $h_{t}$ is updated based on the previous outputs of the network. While a simple recurrent network is just a feedforward network with the hidden state concatenated to the input and sliced off of the output, more sophisticated “recurrent cells” exist (such as gated recurrent units and long short-term memory) that use tailored internal architectures to more carefully manage how the hidden state is updated with each input.
A sequence-to-sequence encoder/decoder model consists of two RNNs: an encoder RNN and a decoder RNN. An unrolled version of this architecture is shown below:
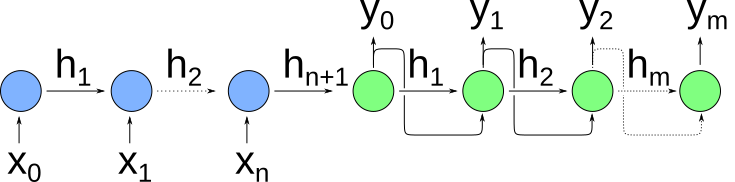
The blue cells are the “encoder” RNNs, and the green cells are the “decoder” RNNs. Note that in contrast to our generic RNN depicted above, in the encoding step we only care about the hidden state, not the output of the cell. The idea is that as the encoder processes a sequence of inputs, it builds up a hidden state encoding that entire sequence, which is then passed along to the decoder network. This final hidden state ($h_{n+1}$ above) is called the context, and it is what’s passed as the initial input to the decoder. The decoder then produces outputs from this initial hidden state, where each output is used as the input for generating the subsequent output.
One interesting feature of this approach is that the input and output sequences may be different lengths—in fact, typically outputs are generated from the decoder until the decoder produces an “end of sequence” token. This is particularly useful in cases where variable-length sequences are desirable, such as language translation. For example, the phrase “veni, vidi, vici” in Latin translates to “I came, I saw, I conquered” in English, and the English rendition of the phrase has double the number of words.
In practice, this approach has a major shortcoming: in order for it to work, the context vector (the final hidden state) must capture all of the relevant information from the input sequence. Because the hidden state of the encoder is built up iteratively with each input token, it is often difficult for the decoder to produce appropriate outputs when the input sequence is long and the information needed to produce a given output appears much earlier in the input sequence. This can be mitigated somewhat by using a high-dimensional context, and by careful choice of recurrent cells (e.g. LSTMs). Sequence-to-sequence models like the one described above can be further improved through the addition of an attention mechanism that allows the decoder cells to inspect the hidden states of the input at each step. Essentially, attention adds an additional feedforward network that uses the decoder’s hidden state to select which of the encoder’s hidden states is most relevant to producing the current term in the output sequence. (Red cells, below.)
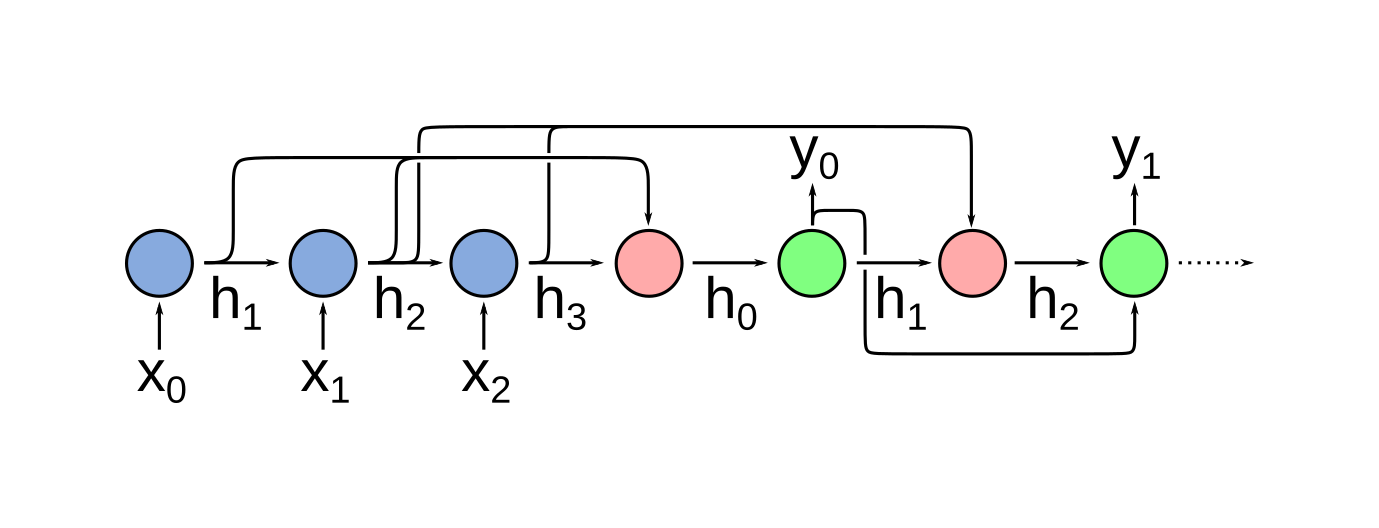
However, the current state of the art approach (used in, for example, GPT-3) relies on a “transformer” architecture that actually dispenses with the recurrent components of these sequence-to-sequence models entirely (see “Attention is all you need” for more details).
My terrible model
For this exercise, I decided to start with the simplest approach: implement a basic (attention-free) encoder-decoder sequence-to-sequence model from scratch. To start, I needed a suitable dataset for modeling. After some googling, I found the “Aligned Hansards of the 36th Parliament of Canada”, which contains approximately 1.3 million English-French pairs of aligned text chunks from the official records of the 36th Canadian parliament. Downloading, extracting, and processing this data into a suitable form for modeling was straightforward:
english_debates = sorted(glob.glob(directory + "*.e.gz"))
french_debates = sorted(glob.glob(directory + "*.f.gz"))
english_txt = []
french_txt = []
for i, (e_deb, f_deb) in enumerate(zip(english_debates, french_debates)):
with gzip.open(e_deb) as f:
eng_lines = f.read().decode("utf-8", errors="ignore").split("\n")
with gzip.open(f_deb) as f:
fre_lines = f.read().decode("utf-8", errors="ignore").split("\n")
if len(eng_lines) == len(fre_lines):
english_txt += eng_lines
french_txt += fre_lines
else:
print("Mismatched lines in file: {}".format(e_deb))
if i % 50 == 0:
print("{}/{}".format(i + 1, len(english_debates)))
Check that it worked:
english_txt[125]
'It is my duty to inform the House that the Speaker of this House has ... '
I then applied some simple preprocessing (cast to lowercase, split on spaces and punctuation, drop all non-word characters) to transform sentences like the above into arrays:
['it', 'is', 'my', 'duty', 'to', 'inform', 'the', 'house', 'that', ...]
This was the source of my first mistake.
Mistake 1: Picking the wrong data for the problem
My goal was to build a model to translate simple English phrases into French ones. But, the dataset I’d picked was the minutes of parliamentary debates—not very representative of simple conversational English or French. In fact, there were more than 30,000 English words in the vocabularly after my preprocessing, but many everyday words were missing. Note that this is not intended as a criticism of the intrinsic quality of the Hansard dataset, only its suitability for the task at hand!
It wasn’t just a problem that many common words are missing from this dataset: another issue is that patterns of formal speech (such as might be used in, say, a parliamentary debate) tend to be different from day-to-day speech. For example, in the sentence above (“it is my duty to inform the House that…”), the word “house” is not being used to refer to a home or residence, it’s referring to a legislative body.
After recognizing this, I searched for another dataset, and eventually found this curated collection of sentence pairs from the Tatoeba Project. On top of this, I also updated my preprocessing code to restrict to a limited subset of sentences. Here’s a snippet:
import re
from collections import Counter
import pandas as pd
def tokenize(s):
tokens = re.split(r'\W+', s.lower())
tokens = [re.sub(r' +', '', t) for t in tokens]
return ["<SOS>"] + [t for t in tokens if len(t) > 0] + ["<EOS>"]
df = pd.read_csv("fra-eng/fra.txt",
sep="\t",
header= None,
names=["en", "fr", "note"])
english_sentences = [tokenize(x) for x in df["en"]]
french_sentences = [tokenize(x) for x in df["fr"]]
for s in english_sentences:
en_counter.update(w for w in s)
for s in french_sentences:
fr_counter.update(w for w in s)
en_words = set([w for w, c in en_counter.most_common()[0:2000]])
fr_words = set([w for w, c in fr_counter.most_common()[0:2000]])
pairs = []
for en_s, fr_s in zip(english_sentences, french_sentences):
if len(en_s) > 10 or len(fr_s) > 10:
continue
skip = False
for w in en_s:
if w not in en_words:
skip = True
break
for w in fr_s:
if w not in fr_words:
skip = True
break
if skip:
continue
pairs.append((en_s, fr_s))
There are a few things going on here:
- I’m dropping all non-word characters when I tokenize the strings, and inserting “start of sequence” and “end of sequence” tokens.
- I’m calculating word frequencies for each word appearing in each language (using Python’s
collections.Counterclass). - I’m restricting the vocabulary for each language to only the 2,000 most common words in the corpus.
- I am only matching pairs of sentences that each contain less than 10 tokens (less than 8 words, because of the sequence delimiters), and only contain words from the restricted vocabulary.
After doing all this, I’m left with 63,123 sentence pairs, all of which are very simple.
For example, pair 12345 is the matched statements:
['<SOS>', 'you', 're', 'the', 'leader', '<EOS>'] # English
['<SOS>', 'c', 'est', 'toi', 'la', 'chef', '<EOS>'] # French
Encoding/Decoding Sentences
To play nicely with PyTorch’s standard embedding layer, I needed to assign a unique integer to each token. There might be some kind of “bidirectional map” in the standard library, but I implemented a custom class for this:
class Vocab(object):
def __init__(self):
self.w2i = {}
self.i2w = {}
def fit(self, sentences):
i = 0
for sent in sentences:
for word in sent:
if word not in self.w2i:
self.w2i[word] = i
self.i2w[i] = word
i += 1
return
def __len__(self):
return len(self.w2i)
def encode(self, sentence):
return [self.w2i[w] for w in sentence]
def decode(self, array):
return [self.i2w[i] for i in array]
Use it like this:
en_vocab = Vocab()
en_vocab.fit([x for x, _ in pairs])
# sentence: ['<SOS>', 'i', 'have', 'to', go', '<EOS>']
en_vocab.encode(pairs[2100][0])
# returns [0, 9, 178, 160, 1, 2]
Note that after fitting, there are only 1821 tokens in the English vocabulary and 1987 tokens in the French one.
Mistake 2: Fixed sequence implementation
Although I wanted to write this one in PyTorch, I’d worked with LSTMs previously in Keras several years ago, and this influenced my initial attempt at implementation. My previous experience with recurrent nets had relied on fixed-length sequences, where null tokens are inserted for input sequences that don’t reach the full input length. My hand-rolled PyTorch RNN followed a similar pattern:
class BadRNN(nn.Module):
def __init__(self, input_size, hidden_size, num_layers):
super().__init__()
self.layers = nn.ModuleList([nn.Linear(input_size + hidden_size,
input_size + hidden_size,
bias=True)
for _ in range(0, num_layers)])
self.hidden_size = hidden_size
self.input_size = input_size
# x is shape (batch_size, n_layers, vector)
def forward(self, x, h=None):
if h is None:
h = torch.zeros((x.shape[0], self.hidden_size),
device=x.device,
requires_grad=True)
x_out = torch.zeros((x.shape[0], len(self.layers), self.input_size),
device=x.device)
for i, fc in enumerate(self.layers):
x_in = x[:,i,:]
out = F.tanh(torch.cat((h, x_in), 1))
h = out[:,:self.hidden_size]
x_out[:,i,:] = out[:,self.hidden_size:]
return x_out, h
There’s a glaring error with this implementation: I’ve assigned separate parameters for each step in the sequence.
self.layers consists of num_layers copies of fully connected linear weights.
This means that I’m assigning a unique set of parameters to each step in my encoder/decoder, rather than re-using the same set of weights at each step.
The correct implementation would be to drop the nn.ModuleList and replace it with a single nn.Linear module (or perhaps a GRU or LSTM module instead).
In addition to the fixed sequence length (num_layers) and flawed implementation, the other disadvantage of this approach is that it’s not amenable to teacher forcing.
Teacher forcing is a training technique in which, rather than feeding the decoder RNN’s outputs as inputs to produce the next decoder output, the decoder RNN is given the correct output for the previous step.
This can improve training times and accuracy, particularly for longer sequences.
Thanks to PyTorch’s eager evaluation, restricting to fixed-length sequences actually isn’t necessary at all: we can freely vary the length of the input and output sequences at training time as needed. To facilitate this, I ended up with something very close to the PyTorch seq2seq tutorial’s implementation for my encoder and decoder RNNs.
class Encoder(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(input_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size)
def forward(self, x, h):
x = self.embedding(x).view(1,1,-1)
x, h = self.gru(x, h)
return x, h
class Decoder(nn.Module):
def __init__(self, hidden_size, output_size):
super().__init__()
self.hidden_size = hidden_size
self.embedding = nn.Embedding(output_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size)
self.out = nn.Linear(hidden_size, output_size)
self.softmax = nn.LogSoftmax(dim=1)
def forward(self, x, h):
x = self.embedding(x).view(1,1,-1)
x = F.relu(x)
x, h = self.gru(x, h)
x = self.softmax(self.out(x[0]))
return x, h
Note that I decided to use a GRU rather than a simple feedforward layer inside my RNNs.
Mistake 3: Training with single examples
At this point, since I was hewing very close to the PyTorch seq2seq tutorial, I decided to re-use their training code as well. The tutorial contains this snippet:
teacher_forcing_ratio = 0.5
def train(input_tensor, target_tensor,
encoder, decoder, encoder_optimizer, decoder_optimizer,
criterion, max_length=MAX_LENGTH):
encoder_hidden = encoder.initHidden()
encoder_optimizer.zero_grad()
decoder_optimizer.zero_grad()
input_length = input_tensor.size(0)
target_length = target_tensor.size(0)
encoder_outputs = torch.zeros(max_length, encoder.hidden_size,
device=device)
loss = 0
for ei in range(input_length):
encoder_output, encoder_hidden = encoder(
input_tensor[ei], encoder_hidden)
encoder_outputs[ei] = encoder_output[0, 0]
decoder_input = torch.tensor([[SOS_token]], device=device)
decoder_hidden = encoder_hidden
use_teacher_forcing = True if random.random() < teacher_forcing_ratio else False
if use_teacher_forcing:
# Teacher forcing: Feed the target as the next input
for di in range(target_length):
decoder_output, decoder_hidden, decoder_attention = decoder(
decoder_input, decoder_hidden, encoder_outputs)
loss += criterion(decoder_output, target_tensor[di])
decoder_input = target_tensor[di] # Teacher forcing
else:
# Without teacher forcing: use its own predictions as the next input
for di in range(target_length):
decoder_output, decoder_hidden, decoder_attention = decoder(
decoder_input, decoder_hidden, encoder_outputs)
topv, topi = decoder_output.topk(1)
decoder_input = topi.squeeze().detach() # detach from history as input
loss += criterion(decoder_output, target_tensor[di])
if decoder_input.item() == EOS_token:
break
loss.backward()
encoder_optimizer.step()
decoder_optimizer.step()
return loss.item() / target_length
When I attempted to use this in my own code mutatis mutandis, my model did not converge in any reasonable span of time. I suspect the problem is that this training function performs a weight update after every single input. Maybe this doesn’t cause problems when the model includes attention, but it definitely screwed up my seq2seq model!
I modified this loop to update on batches of 64 pairs at a time. After 1,000 batches, I arrived at something reasonable. Here’s my updated training loop.
train_losses = []
criterion = nn.NLLLoss()
teacher_forcing_ratio = 0.5
t0 = time.time()
for k in range(0, 1_000):
enc_optimizer.zero_grad()
dec_optimizer.zero_grad()
loss = 0
for _ in range(0, 64):
x, y, _ = gen_example()
x = torch.tensor(list(reversed(x)), dtype=torch.long, device=device)
# first element is always <SOS>
y = torch.tensor(y[1:], dtype=torch.long, device=device).view(-1,1)
h = torch.zeros((1,1, 1024), device=device)
enc_outputs = torch.zeros(x.shape[0],
encoder.hidden_size,
device=device)
for ei in range(x.shape[0]):
_, h = encoder(x[ei], h)
dec_input = torch.tensor([fr_vocab.encode(["<SOS>"])], device=device)
use_teacher_forcing = True if random.random() < teacher_forcing_ratio else False
if use_teacher_forcing:
for di in range(y.shape[0]):
dec_output, h = decoder(dec_input, h)
loss += criterion(dec_output, y[di])
else:
for di in range(y.shape[0]):
dec_output, h = decoder(dec_input, h)
topv, topi = dec_output.topk(1)
# detach from history as input
dec_input = topi.squeeze().detach()
loss += criterion(dec_output, y[di])
if dec_input.item() == fr_vocab.encode(["<EOS>"])[0]:
break
loss.backward()
enc_optimizer.step()
dec_optimizer.step()
if k % 10 == 0:
print("step: {} loss: {} ({:.2f} sec)".format(k,
loss.item()/64.0,
time.time() - t0))
t0 = time.time()
train_losses.append(loss.item()/64.0)
Note that I’m also passing along the reversed input sequence (so that the last token passed to the encoder is the first token in the input sequence). Empirically, I found that I got slightly better results doing it this way, but I’m not sure what the linguistic justification could be.
Finally, a working model?
I got reasonable convergence from training, although with a bit of jitter:
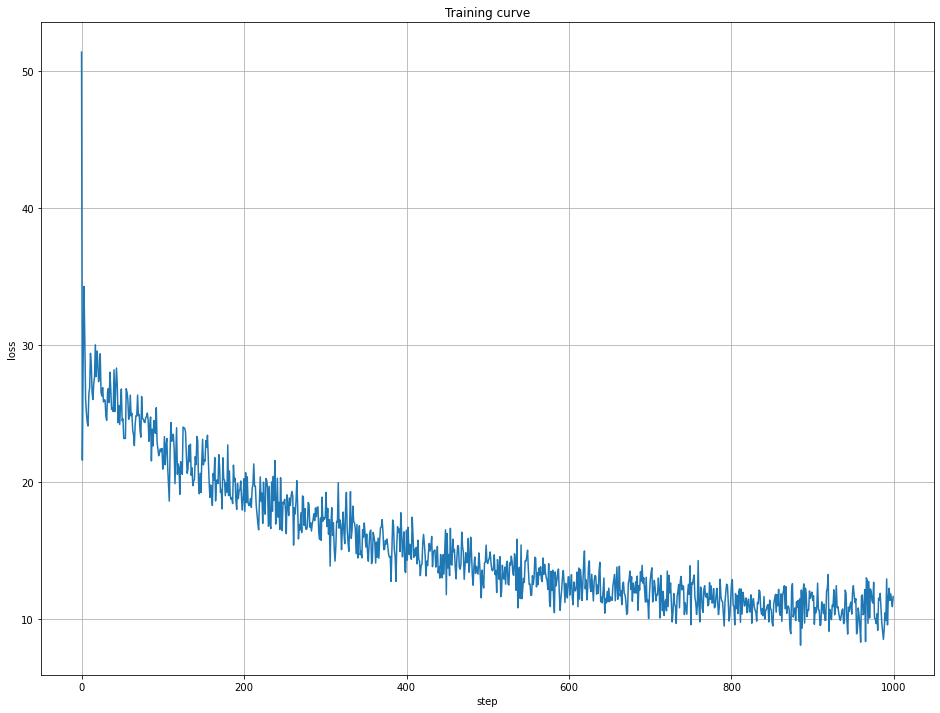
But before I could be satisfied, I had to check that it was actually producing something close to reasonable.
I wrote a predict function that would translate a sentence in English into one in French, using our seq2seq model:
def predict(sentence):
inputs = en_vocab.encode(tokenize(sentence))
outputs = []
with torch.no_grad():
x = torch.tensor(list(reversed(inputs)),
dtype=torch.long,
device=device)
h = torch.zeros((1, 1, 1024), device=device)
for ei in range(x.shape[0]):
_, h = encoder(x[ei], h)
dec_input = torch.tensor([fr_vocab.encode(["<SOS>"])], device=device)
output = None
count = 0
while output != "<EOS>" and count < 25:
dec_output, h = decoder(dec_input, h)
topv, topi = dec_output.topk(1)
dec_input = topi.squeeze().detach()
output = fr_vocab.decode([dec_input.item()])[0]
outputs.append(output)
count += 1
return " ".join(outputs[:-1])
First, let’s test it with an example from the pairs of sentences.
Element 1234 in pairs is
['<SOS>', 'he', 'grew', 'old', '<EOS>']
['<SOS>', 'il', 'est', 'devenu', 'vieux', '<EOS>']
Calling predict:
predict("he grew old")
# returns 'il devint vieux'
Google Translate suggests that this means “he got old” in English, so it seems like we’re on the right track. (Mistake 4: I don’t actually know French!)
A few more “translations” from the model:
"I love you" > "je t aime"
(Even I know that one is correct!) The model stumbled on this next one:
"The dog ran fast" > "le chien a été"
It gets “the dog” correct (“le chien”), but whiffs on the rest of the sentence.
Finally I tried
"I learned a lot today" > "j ai appris beaucoup aujourd aujourd"
I’m not sure why “aujourd” (“today”) came out twice—apparently, conditioned on the context at that step and the previous word being “aujourd”, the decoder believes “aujourd” is likely to follow.
Anyway, that concludes this seq2seq model implementation catastrophe. Adding attention would probably be a good idea, and the official PyTorch tutorial will walk you through how to do that. In the meantime, if you’re looking to implement your own seq2seq model, hopefully you’ve learned from my mistakes and will have better luck than I did!